דף נוסחאות
| מבוא | תנועה בקו ישר | תנועה במישור | תנועה מעגלית | חוקי ניוטון | חוקי ניוטון ב׳ | תנועה הרמונית | עבודה ואנרגיה | מתקף ותנע |
- יחידות מידה:
היחידות הבסיסיות הן \(M,K,S\):
\(M\)- מטר [\(m\)]
\(K\)- קילוגרם [\(kg\)]
\(S\)- שניות [\(sec\)]
תחיליות נפוצות:
\(k=1000=10^3\)
\(c=\frac{1}{100}=10^{-2}\)
\(m=\frac{1}{1000}=10^{-3}\) - משולש ישר זווית:
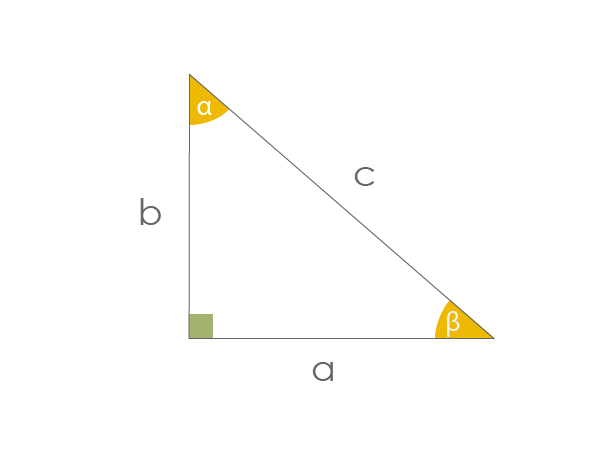
\(sin\alpha=\frac{a}{c}\)
\(cos\alpha=\frac{b}{c}\)
\(tan\alpha=\frac{a}{b}\)
משפט פיתגורס: \(c^2=a^2+b^2\) - זהויות טריגונומטריות בסיסיות:
\(sin^2\alpha+cos^2\alpha=1\)
\(cos(90^\circ-\alpha)=sin\alpha\)
\(sin(90^\circ-\alpha)=cos\alpha\)
\(sin2\alpha=2cos\alpha sin\alpha\) - משולש כללי:
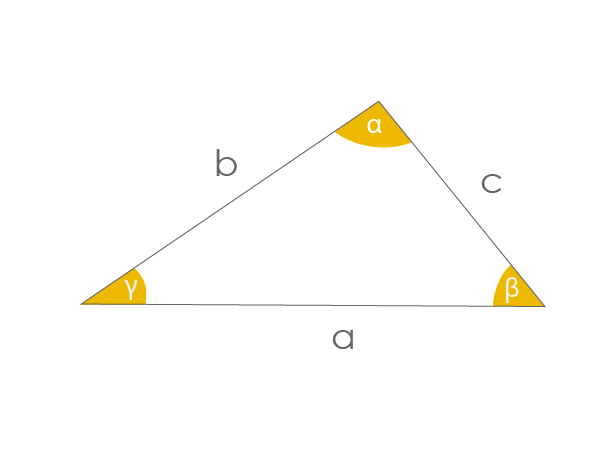
משפט הקוסינוסים:
\(c^2=a^2+b^2-2abcos\alpha\)
משפט הסינוסים:
\(\frac{a}{sin\alpha}=\frac{b}{sin\beta}=\frac{c}{sin\gamma}\)
- העתק:
\(\Delta x=x_2-x_1\) - תנועה במהירות קבועה:
\(v=\frac{\Delta x}{\Delta t}\)
\(x_t=x_0+v\cdot t\) - גרף ליניארי:
הפונקציה הליניארית \(y=a+bx\)
\(b=\frac{\Delta y}{\Delta x}\) - מהירות ממוצעת:
\(\overline{v}=\frac{\Delta x}{\Delta t}\) - מהירות רגעית:
\(v=\frac{\Delta x}{\Delta t}_{\Delta t \rightarrow 0}=\frac{dx}{dt}\) - תאוצה ממוצעת:
\(\overline{a}=\frac{\Delta v}{\Delta t}\) - תאוצה רגעית:
\(a=\frac{\Delta v}{\Delta t}_{\Delta t \rightarrow 0}=\frac{dv}{dt}=\frac{d^2x}{dt^2}\) - נגזרות נפוצות:
כאשר \(C\) קבוע.
\(\frac{dC}{dt}=0\)
\(\frac{d(Ct)}{dt}=C\)
\(\frac{d(Ct^2)}{dt}=2Ct\)
\(\frac{d(Ct^n)}{dt}=Cnt^{n-1}\) -
כללי גזירה בסיסיים:
כאשר \(A(t),B(t)\) הן שתי פונקציות כלליות התלויות בזמן:
1. נגזרת של סכום (או הפרש) של פונקציות:
\(\frac{d}{dt}(A(t)+B(t))=\frac{dA(t)}{dt}+\frac{dB(t)}{dt}\)
2. נגזרת של פונקציה כפול קבוע:
\(\frac{d(C \cdot A(t))}{dt}=C \cdot \frac{dA(t)}{dt}\)
3. נגזרת מכפלה:
\(\frac{d}{dt}(A(t) \cdot B(t))=A(t) \cdot \frac{dB(t)}{dt}+B(t) \cdot \frac{dA(t)}{dt}\)
4. נגזרת מנה:
\(\frac{d}{dt}(\frac{A(t)}{B(t)})=\frac{\frac{d}{dt}(A(t)) \cdot B(t)-\frac{d}{dt}(B(t)) \cdot A(t)}{B^2(t)}\)
5. נגזרת מורכבת:
\(\frac{d}{dt}(A(B(t)))=\frac{d}{dt}(A(B(t))) \cdot \frac{dB(t)}{dt}\)
- אינטגרל בבעיות תנועה:
\(x=\int vdt\)
\(v=\int atd\) - כללי אינטגרציה:
נדגים זאת עבור שתי הפונקציות הכלליות \(A(t)\) ו-\(B(t)\).
1. אינטגרל של פונקציה כפול קבוע:
\(\int{C \cdot A(t)dt}=C \cdot \int{A(t)dt}\)
2. אינטגרל של סכום או הפרש פונקציות:
\(\int{(A(t)+B(t))dt}=\int{A(t)dt}+\int{B(t)dt}\)
- תנועה בתאוצה קבועה:
\(x_t=x_0+v_0t+\frac{1}{2}at^2\)
\(v_t=v_0+at\)
\(v_t^2=v_0^2+2a(x_t-x_0)\)
\(x_t=x_0+(\frac{v_0+v_t}{2})t\) - פונקציה ריבועית:
\(y=c+bx+ax^2\)
- ווקטור המיקום:
\(\vec{r}=r_x\hat{x}+r_y\hat{y}\) - העתק:
\(\Delta \vec{r}=\Delta x\hat{x}+\Delta y\hat{y}\) - מהירות:
\(\vec{v}=\frac{\Delta \vec{r}}{\Delta t}=\frac{\Delta x}{\Delta t}\hat{x}+\frac{\Delta y}{\Delta t}\hat{y}\)
\(\vec{v}_{\Delta t \rightarrow 0}=\frac{dx}{dt}\hat{x}+\frac{dy}{dt}\hat{y}=v_{xt}\hat{x}+v_{yt}\hat{y}\) - תאוצה:
\(\vec{a}=\frac{\Delta \vec{v}}{\Delta t}=\frac{\Delta v_x}{\Delta t}\hat{x}+\frac{\Delta v_y}{\Delta t}\hat{y}\)
\(\vec{a}_{\Delta t \rightarrow 0}=\frac{dv_{xt}}{dt}\hat{x}+\frac{dv_{yt}}{dt}\hat{y}=a_{xt}\hat{x}+a_{yt}\hat{y}\) - בהינתן \(\vec{v_0},\vec{r_0},\vec{a}\):
\(\vec{v}=(\int{a_xdt})\hat{x}+(\int{a_ydt})\hat{y}\)
\(\vec{r}=(\int{v_xdt})\hat{x}+(\int{v_ydt})\hat{y}\)
- המרה ממעלות לרדיאנים:
\(\Theta(rad)=\frac{\Theta(deg)\cdot 2\pi}{360^\circ}\) - אורך קשת:
\(S=\Theta R\) - פונקציית \(sin\):
\(Asin(\omega t+\phi)\) - זמן מחזור:
\(T=\frac{2\pi}{\omega}\) - הפונקציות \(sin,cos\)- נגזרות ואינטגרלים:
\(\frac{d}{dt}(sint)=cost\)
\(\frac{d}{dt}(cost)=-sint\)
\(\int{sintdt}=-cost+C\)
\(\int{costdt}=sint+C\) - תנועה מעגלית במהירות קבועה:
\(\vec{r}=Rcos(\omega t)\hat{x}+Rsin(\omega t)\hat{y}\)
\(|\vec{r}|=R\)
\(\vec{v}=-R\omega sin(\omega t)\hat{x}+R\omega cos(\omega t)\hat{y}\)
\(|\vec{v}|=\omega R\)
\(\vec{a}=-\omega^2Rcos(\omega t)\hat{x}-\omega^2 Rsin(\omega t)\hat{y}\)
\(\vec{a}=-\omega^2\vec{r}\)
\(|\vec{a}|=\omega^2R=\frac{v^2}{R}\) - תנועה מעגלית מוכללת:
\(\vec{r}=Rcos(\Theta_t)\hat{x}+Rsin(\Theta_t)\hat{y}\)
\(\omega_t=\frac{d\Theta_t}{dt}\)
\(\vec{v}=-R\omega_t sin(\Theta_t)\hat{x}+R\omega_t cos(\Theta_t)\hat{y}\)
\(|\vec{v}|=R\omega_t\)
\(\alpha_t=\frac{d\omega_t}{dt}\)
\(\vec{a}=-\omega_t^2\vec{r}+\frac{\alpha_t}{\omega_t}\vec{v}\)
\(|\vec{a_R}|=\omega_t^2R\)
\(|\vec{a_T}|=\alpha_tR\)
- החוק הראשון של ניוטון:
\(\Sigma \vec{F} \iff \vec{a}=0\)
\(\Sigma F_x \iff a_x=0\)
\(\Sigma F_y \iff a_y=0\) - החוק השני של ניוטון:
\(\Sigma \vec{F}=m\vec{a}\)
\(\Sigma F_x=ma_x\)
\(\Sigma F_y=ma_y\) - החוק השלישי של ניוטון:
\(\vec{F_{1,2}}=-\vec{F_{2,1}}\) - כוח החיכוך:
\(f_{s,max}=\mu_s\cdot N\)
\(f_k=\mu_k\cdot N\)
\(\mu_s \geq \mu_k\)
- חוק הכבידה האוניברסלי:
\(F=G\frac{m_1\cdot m_2}{r^2}\)
\(G=6.67\cdot 10^{-11}\frac{Nm^2}{kg^2}\) - תאוצת הכובד:
\(a=\frac{GM}{r^2}\) - כוחות בתנועה מעגלית:
\(\Sigma F_R=ma_R=m\omega^2R=\frac{mv^2}{R}\)
\(\Sigma F_T=ma_T=m\alpha R\)
- חוק הוק:
\(\vec{F}=-k\vec{x}\) - תנועה הרמונית:
המשוואה הדיפרנציאלית המתארת את התנועה ההרמונית:
\(\frac{d^2x_t}{dt^2}=-\omega^2x_t\)
\(\omega^2=\frac{k}{m}\)
\(x(t)=Acos(\omega t+\phi)\)
\(v(t)=-A\omega sin(\omega t+\phi)\)
\(a(t)=-A\omega^2cos(\omega t+\phi)\) - זמן מחזור:
\(T=\frac{2\pi}{\omega}\) - תדירות:
\(f=\frac{1}{T}\) - קפיץ אנכי:
\(F=mg-kx=-ku\)
\(u=x-\frac{mg}{k}\)
\(u(t)=Acos(\omega t+\phi)\)
\(x(t)=u(t)+\frac{mg}{k}\) - מטוטלת:
המשוואה הדיפרנציאלית המתארת את תנועת המטוטלת:
\(\frac{d^2\Theta}{dt^2}=-\frac{g}{l}sin\Theta\)
עבור זוויות קטנות:
\(sin\Theta \sim \Theta\)
\(\frac{d^2\Theta}{dt^2}=-\Omega^2 \Theta\)
\(\Omega^2=\frac{g}{l}\)
- עבודה:
\(W=|\vec{F}|cos\alpha|\Delta \vec{x}|=\vec{F}\cdot \Delta \vec{x}\) - מכפלה סקלרית:
\(\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|cos\alpha\) - סכום העבודות:
\(\Sigma W=W_1+W_2+....\) - עבודת הכוח השקול:
\(W_{F_T}=\vec{F_T}\cdot \Delta \vec{x}\) - משפט עבודה אנרגיה קינטית:
\(E_k=\frac{1}{2}mv^2\)
\(W_{F_T}=\Delta E_k\) - עבודה של כוח לא קבוע:
\(W=\int^{x_2}_{x_1}\vec{F}\cdot \vec{dx}\) - אנרגיה פוטנציאלית:
\(E_p=-\int\vec{F}\cdot \vec{dx}\) - אנרגיה פוטנציאלית של כוח הכובד:
\(E_p=mgh\) - אנרגיה פוטנציאלית של קפיץ:
\(E_p=\frac{1}{2}kx^2\) - עבודה של \(\vec{F}\):
\(W_F=-\Delta E_p\) - חוק שימור האנרגיה:
\(E_T=E_k+E_{p_1}+E_{p_2}+....\)
\(\Delta E_T=W_{n.c}\) - תנועה מעגלית אנכית:
\(N_{\Theta}=mgcos\Theta+\frac{mv_{\Theta}^2}{R}\)
\(v_{\Theta,min}=\sqrt{-Rgcos\Theta}\)
בנקודה העליונה ביותר:
\(v_{\Theta,min}=v_c=\sqrt{Rg}\)
- תנע:
\(\vec{p}=m\vec{v}\) - תנע של מערכת:
\(\vec{p_1}+\vec{p_2}+\vec{p_3}+...\) - חוק שימור התנע:
כאשר אין כוחות חיצוניים על המערכת:
\(\vec{p_1}+\vec{p_2}+...=const\) - התנגשויות:
\(m_1\vec{v_1}+m_2\vec{v_2}=m_1\vec{u_1}+m_2\vec{u_2}\)\ - התנגשות פלסטית:
\(m_1\vec{v_1}+m_2\vec{v_2}=(m_1+m_2)\vec{u}\) - התנגשות אלסטית:
\(v_1-v_2=u_2-u_1\)
